Riddler Baseball
Mar 22, 2019
Introduction
This week's riddler asks us to simulate a game of baseball using rolls of a dice. To solve this problem, we're going to treat the game of Baseball like a markov chain. To borrow an analogy from one of my favorite professors (Hi, Dr. Popescu!), a markov chain is like a frog hopping among lily pads. The frog has what's called a "current state" - that is, the lily pad it is currently occupying. The frog also has a random probability of hopping to any of the lily pads around it, including some probability of staying where it is. Once the frog hops to a new lily pad, it might have different probabilities of hopping to other lily pads, and this process continues for as long as we like. However, a key property of this system is that we only need to know the current state of the frog in order to estimate where it will go next. It doesn't matter how the frog got to its current state. It may have taken hundreds of hops or just a single hop to arrive in its current state, but that doesn't affect the frog's likelihood of moving to other lily pads. This simplifies the modeling process because we don't need to keep track of the history of events over time - we just need to know where we are and the probabilities of moving to new states.
Here's the problem we're given. Next, we'll outline the steps to solve it.
Over the years, people have invented many games that simulate baseball using two standard dice. In these games, each dice roll corresponds with a baseball event. Two players take turns rolling dice and tracking what happens on the field. Suppose you happen to be an ardent devotee of one of these simulated games from the late 19th century, called Our National Ball Game, which assigns rolls to baseball outcomes like so:
- 1, 1: double
- 1, 2: single
- 1, 3: single
- ... other rolls... we'll examine the full list later
- 5, 6: triple
- 6, 6: home run
Given those rules, what’s the average number of runs that would be scored in nine innings of this dice game? What’s the distribution of the number of runs scored? (Histograms welcome.) You can assume some standard baseball things, like runners scoring from second on singles and runners scoring from third on fly outs.
Markov Chain Baseball
Under the simplified dice framework, we can treat the game of baseball like a markov chain that has a current state, a set of transition probabilities to subsequent states, and associated payoffs (runs scored) when certain states are reached. Using this paradigm, we can simulate innings probabilistically, count the runs scored by each team, and determine the winner. Let's walk through exactly how we turn the game of baseball into a markov chain by describing the different components we'll need.
- Current state - describes the strike count for the current batter, the number of outs, and the position of any runners on base. A small quirk of this game: we can only roll for strikes (not balls), so we only need to keep track of the current strikes for our batter. For example, each of these is a valid state of the game.
- 0 strikes, 0 outs, bases empty (starting state each inning)
- 1 strike, 1 out, runner on first
- 2 strikes, 2 outs, bases loaded ... (bottom of the ninth, game seven... just kidding!)
- Additionally, we define the end of the inning as "0 strikes, 3 outs, bases empty". Eventually, every inning will end up here because the probability of staying in this state once we arrive is 100%. In markov chains this is called an "absorbing state" because we can never leave once we arrive.
- Transition probabilities - we simulate game events by rolling dice. For example, rolling a 1 and a 3 (the order doesn't matter) results in a base hit. If we are currently in a state of "0 strikes, 0 outs, bases empty", then we will transition to a new state "0 strikes, 0 outs, runner on first". We know that rolling a (1,3) with two dice will occur with probability . On the other hand, there are four ways to roll a "strike", so the probability of moving from "0 strikes, 0 outs, bases empty" to "1 strike, 0 outs, bases empty" is . It is impossible to move from "0 strikes, 0 outs, bases empty" to "2 strikes, 0 outs, bases empty" in a single move, so the probability is zero. In fact, most of the transition probabilities will be zero, because each game state may only transition to at most 11 other states. Here are several other examples:
- Dice roll (3,1): move from "0 strikes, 0 outs, bases empty" to "0 strikes, 0 outs, runner on first"
- Dice roll (1,3): move from "2 strikes, 2 outs, runner on first" to "0 strikes, 2 outs, runners on first and third" (because the runner on first is typically able to make it to third on a base hit.)
- Dice roll (1,3): move from "1 strike, 1 out, runner on second" to "0 strikes, 1 out, bases empty" (and we increase the run tally by one, because the runner scored from second on the base hit.)
- Rewards - certain game events score runs for the batting team. We track these runs (typically called "rewards" in the markov chain world), and add them up as we go from state to state. For example, if we move from a state of "0 strikes, 0 outs, bases empty" to "0 strikes, 0 outs, bases empty", it means we rolled a (6,6), and hit a home run. (In fact this is one of the rare cases where we stay in the same state, even though we increase the run count by one. Most other actions move us from one state to a different state.) Therefore, the reward for rolling a (6,6) from the initial state is +1. Here are some other examples:
- Dice roll (1,3): move from "2 strikes, 2 outs, runner on first" to "0 strikes, 2 outs, runners on first and third", no increase in runs.
- Dice roll (1,3): move from "1 strike, 1 out, runner on second" to "0 strikes, 1 out, bases empty". Reward of +1 for the single runner that scored.
- Dice roll (6,6): move from "0 strikes, 2 outs, bases loaded" to "0 strikes, 2 outs, bases empty". Reward of +4 because this was a grand slam.
Now that we have the tools to describe our game, we need to specify all possible states, all possible transitions between states, and the rewards associated with each move. We'll use python to do the heavy lifting. The full code can be found at the bottom of this article.
Creating States
We can simplify the task of creating all states by taking advantage of independence among state components. For example, runners on base is independent from the number of strikes and the number of outs. Therefore, we can generate the possibilities separately and combine them for the overall list. There are three possibilities for strikes on an active batter: 0, 1, or 2. (We don't need the number 3 because if a batter has three strikes, then the next batter is up and we instantly reset to 0.) We also have three possibilities for the number of outs in an active inning: 0, 1, or 2, for the same reason as before. However, we do create a special state with 3 outs to signal the end of the inning. Next, we identify all the possibilities of bases that could be occupied: single runners on first, second, or third, runners on first and second, first and third, second and third, and bases loaded. We can express the runners as a tuple of three integers, where 1 means a base is occupied and 0 means it is empty. For example (0,0,0) is bases empty, (0,1,0) means a runner on second, and (1,1,1) means bases loaded. Once we generate each set of possibilities for strikes, outs, and runners, we can use python to assemble all the unique combinations, which results in a list of length .
To represent the current state, we need a data structure that has an attribute for strikes, outs, and runners. We can use the namedtuple data structure as an easy way to store this data. The code snipped below creates this class and instantiates a single instance representing 0 strikes, 1 out, and runners on first and third.
# create the "Inning" class and instantiate a single instance
Inning = namedtuple('Inning', ['strikes', 'outs', 'runners'])
sample_state = Inning(0, 1, (1,0,1))
Calculating Transition Probabilities
This next part involves some manual work and a bit of baseball assumption-making. The objective is to identify all the ways that we can move from one state to another. If each state could transition to each other state, we would need to calculate probabilities, which would be a tedious task. Instead, we can simplify this number substantially. For example, we know that it's impossible to go directly from 0 strikes to 2 strikes, or from bases empty to bases loaded in a single step. Therefore, many of the transition probabilities between states will be zero, which simplifies our task.
Another benefit of our dice game is that we don't have to deal with complicated probabilities. There are 21 unique combinations of two dice, and each combination is equally likely. Furthermore, several of the outcomes from unique dice rolls are the same ("strike", "out at first", etc.) As a result, each state has at most 11 potential moves to another state. Let's write them out with their effect on the game and the probability (out of 21).
| Game Action | Number of Rolls | State Outcome |
|---|---|---|
| Strike | 4 | Increase strike count (also handle strikeouts and outs when necessary) |
| Out at first | 4 | Runners advance by one; runner on third scores (unless it's the third out); out+=1 |
| Fly out | 3 | Runner on third scores (unless it's the third out); out+=1 |
| Single | 3 | Runners on base advance by two; batter moves to first |
| Foul out | 1 | Runners stay where they are; out+=1 |
| Double play | 1 | If nobody is on base, treat as a single out; otherwise tag out the most advanced two runners |
| Base on error | 1 | All runners advance a single base only |
| Walk | 1 | Batter advances to first; runners advance only if forced |
| Double | 1 | Everyone on base scores; batter advances to second base |
| Triple | 1 | Everyone on base scores; batter advances to third base |
| Home run | 1 | Everyone on base plus the batter scores |
Coding the Game Actions in Python
Now we need to encode how a given state will change as the results of a game action. We'll need 11 functions - one for each game action - that take a starting state as input and return the ending state and any runs that may have occurred as a result. Here's an example of one of these functions, that describes what happens when there's a "fly out". In this case, we assume a runner on third is able to score (called "tagging up"), but only if the pop fly is the first or second out. If it's the third out, the inning ends without the run counting. As I mentioned above, there is some subjectivity in the outcomes of each game event, and that's part of the fun of this problem!
Also note that the function below takes a single input: the game state, but returns two results: the subsequent game state and the number of runs that were scored. In this way, we can track the game state as it changes, and keep a running total of runs as they occur during the inning. You can find the other 10 game action functions below in the code.
def fly_out(inning):
"""
Update the inning for a fly out
* runner on third scores unless it's the third out
"""
outs = inning.outs + 1
if inning.runners == (0,0,1): runners, runs = (0,0,0), 1
elif inning.runners == (1,0,1): runners, runs = (1,0,0), 1
elif inning.runners == (0,1,1): runners, runs = (0,1,0), 1
elif inning.runners == (1,1,1): runners, runs = (1,1,0), 1
else: runners, runs = inning.runners, 0
if outs > 2:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(0, outs, runners), runs
Running a Single-Inning Simulation
Now we have all the tools we need to track the state of our game, the likelihood of moving to new states, and the rewards associated with certain actions. All innings start with 0 strikes, 0 outs, and bases empty: Inning(0, 0, (0,0,0)). From the starting state, we simulate dice rolls and play the game, updating the game state and tracking runs as we go. Here's a python function that plays a single inning and prints a summary of what happens. Note that the results are randomly generated according to the weighted probabilities described above, so the results will change every time it's run.
def single_inning(verbose=True):
"""
Simulate a single inning until three outs are recorded. Return the number
of runs scored during the inning. If verbose=True, print a "play-by-play"
summary of the inning for each action. If verbose=False, just return runs
"""
state, score = Inning(0, 0, (0,0,0)), 0
while state.outs < 3:
action = np.random.choice(ACTIONS, p=WEIGHTS)
state, runs = globals()[action](state)
score += runs
if verbose:
print(f'{action:15}: {state}, {score} total runs scored')
return score
# sample output
# -------------
# single : Inning(strikes=0, outs=0, runners=(1, 0, 0)), 0 total runs scored
# strike : Inning(strikes=1, outs=0, runners=(1, 0, 0)), 0 total runs scored
# base_on_error : Inning(strikes=0, outs=0, runners=(1, 1, 0)), 0 total runs scored
# triple : Inning(strikes=0, outs=0, runners=(0, 0, 1)), 2 total runs scored
# strike : Inning(strikes=1, outs=0, runners=(0, 0, 1)), 2 total runs scored
# double : Inning(strikes=0, outs=0, runners=(0, 1, 0)), 3 total runs scored
# single : Inning(strikes=0, outs=0, runners=(1, 0, 0)), 4 total runs scored
# fly_out : Inning(strikes=0, outs=1, runners=(1, 0, 0)), 4 total runs scored
# base_on_error : Inning(strikes=0, outs=1, runners=(1, 1, 0)), 4 total runs scored
# double_play : Inning(strikes=0, outs=3, runners=(0, 0, 0)), 4 total runs scored
Conclusion: Answering the Question
... what’s the average number of runs that would be scored in nine innings of this dice game? What’s the distribution of the number of runs scored?
Now that we can simulate a single inning, we can answer the question by repeating our simulation a large number of times to estimate the long-term distribution of runs scored. Fortunately, each inning is independent (at least in our dice game - no momentum or slumps to worry about). Therefore, if we accurately simulate a single inning, we can accurately simulate a single game by multiplying by nine.
Perhaps the truly detail-oriented among you may note that this answer isn't entirely correct because it precludes the possibility of extra innings. There is a small probability that both teams score the same number of runs after nine innings. If that happened, they would continue playing one inning at a time until one team wins. I may save this small addendum for a separate update later.
def simulate_innings(trials):
"""Simulate a large number of innings and return the total runs scored"""
return np.array([single_inning(verbose=False) for _ in range(trials)])
# sample output of 1 million innings
# ----------------------------------
>>> results = simulate_innings(1000000).mean()
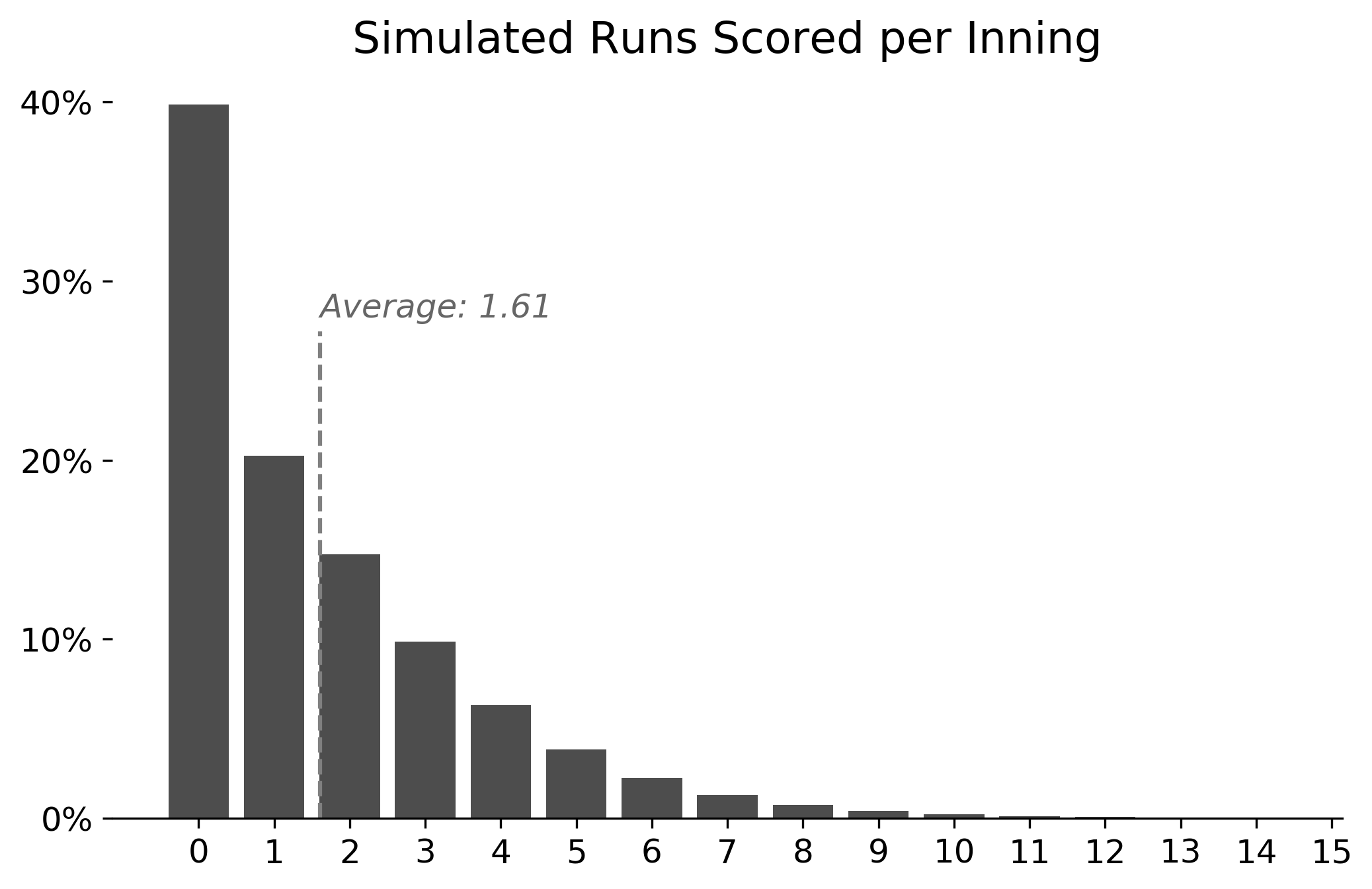
1.611836
Ignoring the small possibility of ties and extra innings, we see that the expected number of runs per inning is roughly 1.61, which means the expected number of runs per nine-inning game is roughly 14.5. According to sportingcharts.com the actual total score of MLB games from 1990 to 2016 hovered between 8-10, which means each team scored between 4 and 5 runs. Our dice game certainly gives the advantage to the sluggers!
What's also interesting is that these results allow us to track not only the average number of runs scored per inning, but the full distribution: how many goose eggs (roughly 40% of the time) vs. quadruple-grand-slams (the highest inning recorded 22 runs). These results are best viewed as a histogram showing exactly how many simulated innings ended up with a given number of runs, which you can see below.
Reference: Full Python Code
"""
Solves the fivethirtyeight Riddler problem from March 22, 2019
Each inning is represented by an object called "Inning", that is comprised of
strikes, outs, and runner positions, e.g. Inning(0, 1, (0,1,0)) for 0 strikes,
1 out, and a runner on second base.
There are 11 unique game actions that can occur. Each is represented by a
function that takes an inning state as input and returns a tuple of the new
inning state after the action and the number of runs that were scored as a
result of the action.
"""
import numpy as np
from collections import namedtuple
# define a container for the current state of an inning
Inning = namedtuple('Inning', ['strikes', 'outs', 'runners'])
# all possible game actions, handled with functions below
__actions__ = [
('strike', 4),
('out_at_first', 4),
('fly_out', 3),
('single', 3),
('base_on_error', 1),
('double', 1),
('double_play', 1),
('foul_out', 1),
('homerun', 1),
('triple', 1),
('walk', 1)
]
ACTIONS = [a[0] for a in __actions__]
WEIGHTS = [float(a[1]) for a in __actions__]
WEIGHTS = [w / sum(WEIGHTS) for w in WEIGHTS]
def single_inning(verbose=True):
"""
Simulate a single inning until three outs are recorded. Return the number
of runs scored during the inning. If verbose=True, print a "play-by-play"
summary of the inning for each action. If verbose=False, just return runs
"""
state, score = Inning(0, 0, (0,0,0)), 0
while state.outs < 3:
action = np.random.choice(ACTIONS, p=WEIGHTS)
state, runs = globals()[action](state)
score += runs
if verbose:
print(f'{action:15}: {state}, {score} total runs scored')
return score
def simulate_innings(trials):
"""Simulate a large number of innings and return the total runs scored"""
return np.array([single_inning(verbose=False) for _ in range(trials)])
def base_on_error(inning):
"""
Update the inning for a base on error
* batter and runners advance one base each
"""
if inning.runners == (0,0,0): runners, runs = (1,0,0), 0
elif inning.runners == (1,0,0): runners, runs = (1,1,0), 0
elif inning.runners == (0,1,0): runners, runs = (1,0,1), 0
elif inning.runners == (0,0,1): runners, runs = (1,0,0), 1
elif inning.runners == (1,1,0): runners, runs = (1,1,1), 0
elif inning.runners == (1,0,1): runners, runs = (1,1,0), 1
elif inning.runners == (0,1,1): runners, runs = (1,0,1), 1
elif inning.runners == (1,1,1): runners, runs = (1,1,1), 1
return Inning(0, inning.outs, runners), runs
def double(inning):
"""
Update the inning for a double
* all runners score; batter advances to second
NOTE: in reality about 50% of runners on first score on a double
"""
return Inning(0, inning.outs, (0,1,0)), sum(inning.runners)
def double_play(inning):
"""
Update the inning for a double play
* if the bases are empty this is treated like a single out; otherwise
it's assumed the two runners farthest advanced are picked off.
"""
if inning.runners == (0,0,0):
# only one out available
runners = (0,0,0)
outs = inning.outs + 1
if inning.runners in [(1,0,0), (0,1,0), (0,0,1)]:
runners = (0,0,0)
outs = inning.outs + 2
elif inning.runners in [(1,1,0), (1,0,1), (0,1,1)]:
runners = (1,0,0)
outs = inning.outs + 2
elif inning.runners == (1,1,1):
runners = (1,1,0)
outs = inning.outs + 2
else:
runners = (0,0,0)
if outs > 2:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(0, outs, runners), 0
def fly_out(inning):
"""
Update the inning for a fly out
* runner on third scores unless it's the third out
"""
outs = inning.outs + 1
if inning.runners == (0,0,1): runners, runs = (0,0,0), 1
elif inning.runners == (1,0,1): runners, runs = (1,0,0), 1
elif inning.runners == (0,1,1): runners, runs = (0,1,0), 1
elif inning.runners == (1,1,1): runners, runs = (1,1,0), 1
else: runners, runs = inning.runners, 0
if outs > 2:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(0, outs, runners), runs
def foul_out(inning):
"""
Update the inning for a foul out
* runners stay where they are
"""
if inning.outs > 1:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(0, inning.outs + 1, inning.runners), 0
def out_at_first(inning):
"""
Update the inning for an out at first
* runners advance one base
"""
outs = inning.outs + 1
if inning.runners == (0,0,0): runners, runs = (0,0,0), 0
elif inning.runners == (1,0,0): runners, runs = (0,1,0), 0
elif inning.runners == (0,1,0): runners, runs = (0,0,1), 0
elif inning.runners == (0,0,1): runners, runs = (0,0,0), 1
elif inning.runners == (1,1,0): runners, runs = (0,1,1), 0
elif inning.runners == (1,0,1): runners, runs = (0,1,0), 1
elif inning.runners == (0,1,1): runners, runs = (0,0,1), 1
elif inning.runners == (1,1,1): runners, runs = (0,1,1), 1
if outs > 2:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(0, outs, runners), runs
def single(inning):
"""
Update the inning for a single
* runners advance two bases; batter advances to first
"""
if inning.runners == (0,0,0): runners, runs = (1,0,0), 0
elif inning.runners == (1,0,0): runners, runs = (1,0,1), 0
elif inning.runners == (0,1,0): runners, runs = (1,0,0), 1
elif inning.runners == (0,0,1): runners, runs = (1,0,0), 1
elif inning.runners == (1,1,0): runners, runs = (1,0,1), 1
elif inning.runners == (1,0,1): runners, runs = (1,0,1), 1
elif inning.runners == (0,1,1): runners, runs = (1,0,0), 2
elif inning.runners == (1,1,1): runners, runs = (1,0,1), 2
return Inning(0, inning.outs, runners), runs
def strike(inning):
"""
Update the inning state for a strike
Returns a new Inning object and the number of runs scored
"""
strikes = inning.strikes + 1
if strikes > 2:
strikes, outs = 0, inning.outs + 1
if outs < 3:
return Inning(strikes, outs, inning.runners), 0
else:
return Inning(0, 3, (0,0,0)), 0
else:
return Inning(strikes, inning.outs, inning.runners), 0
def triple(inning):
"""
Update the inning for a triple
* all runners score; batter advances to third
"""
return Inning(0, inning.outs, (0,0,1)), sum(inning.runners)
def homerun(inning):
"""
Update the inning for a triple
* all runners and the batter score
"""
return Inning(0, inning.outs, (0,0,0)), sum(inning.runners) + 1
def walk(inning):
"""
Update the inning for a walk
* batter advances to first; runners advance if forced
"""
if inning.runners == (0,0,0):
runners, runs = (1,0,0), 0
elif inning.runners in [(1,0,0), (0,1,0)]:
runners, runs = (1,1,0), 0
elif inning.runners == (0,0,1):
runners, runs = (1,0,1), 0
elif inning.runners in [(1,1,0), (1,0,1), (0,1,1)]:
runners, runs = (1,1,1), 0
elif inning.runners == (1,1,1):
runners, runs = (1,1,1), 1
return Inning(0, inning.outs, runners), runs
if __name__ == '__main__':
trials = 1000000
results = simulate_innings(trials)
print(f'Average score from {trials:,.0f} innings: {results.mean():,.2f}')