Riddler Colorful Maze
May 17, 2019
Introduction
This was a colorful Riddler Express. We start with a maze comprised of edges of different colors. Our task is to identify the shortest path from start to finish using only edges of certain colors. This was a great opportunity to take python's networkx library for a spin! We can build the maze as a network, where each edge has a "color" attribute, and use powerful solvers to do the path-finding for us! Here's the full problem text, and the visual to go along with it.
In grade school, you may have learned about the three primary colors — blue, yellow and red — and the three secondary colors — green (blue + yellow), purple (red + blue) and orange (yellow + red).And now it’s time to put that knowledge to use. Try to get through the maze below, a nine-by-nine grid of lines, three times: once as blue, once as yellow, and once as red. If you are blue, you may only travel on lines that include the color blue. So you may travel on lines that are blue, green, purple or white (which contains all colors). You may not travel on orange, yellow, red or black (which contains no colors). The analogous rules hold for your trips as yellow and red.

Coding the maze
I used the fantastic python library networkx to code the maze. In this case, the nodes are fairly unimportant, and we're really interested in the edges; specifically, we're interested in assigning a "color" attribute to each edge. Later, we can use the color attribute to filter the edges for valid pathways, and use networkx's built in solvers to identify the shortest path from start to finish.
The full reference code can be found at the bottom of this article, but the basic approach to codifying the maze is to create an edge between two nodes and assign it a color. For example, this snippet creates the graph and assigns the first eight edges.
import networkx as nx
G = nx.Graph()
G.add_edge((0,0), (0,1), color='o')
G.add_edge((0,1), (0,2), color='w')
G.add_edge((0,2), (0,3), color='g')
G.add_edge((0,3), (0,4), color='w')
G.add_edge((0,4), (0,5), color='y')
G.add_edge((0,5), (0,6), color='w')
G.add_edge((0,6), (0,7), color='y')
G.add_edge((0,7), (0,8), color='w')
Building the graph is the most time-consuming part of the problem. We have to manually assign colors to each of the 144 edges between the nodes to recreate the graph. But once this part is finished the rest of the process is fully automated by the code!
After all that work, we can verify everything is correct by visualizing the graph. The helper function plot_maze takes care of this for us, and produces the image below. It bears a striking resemblance to the original!
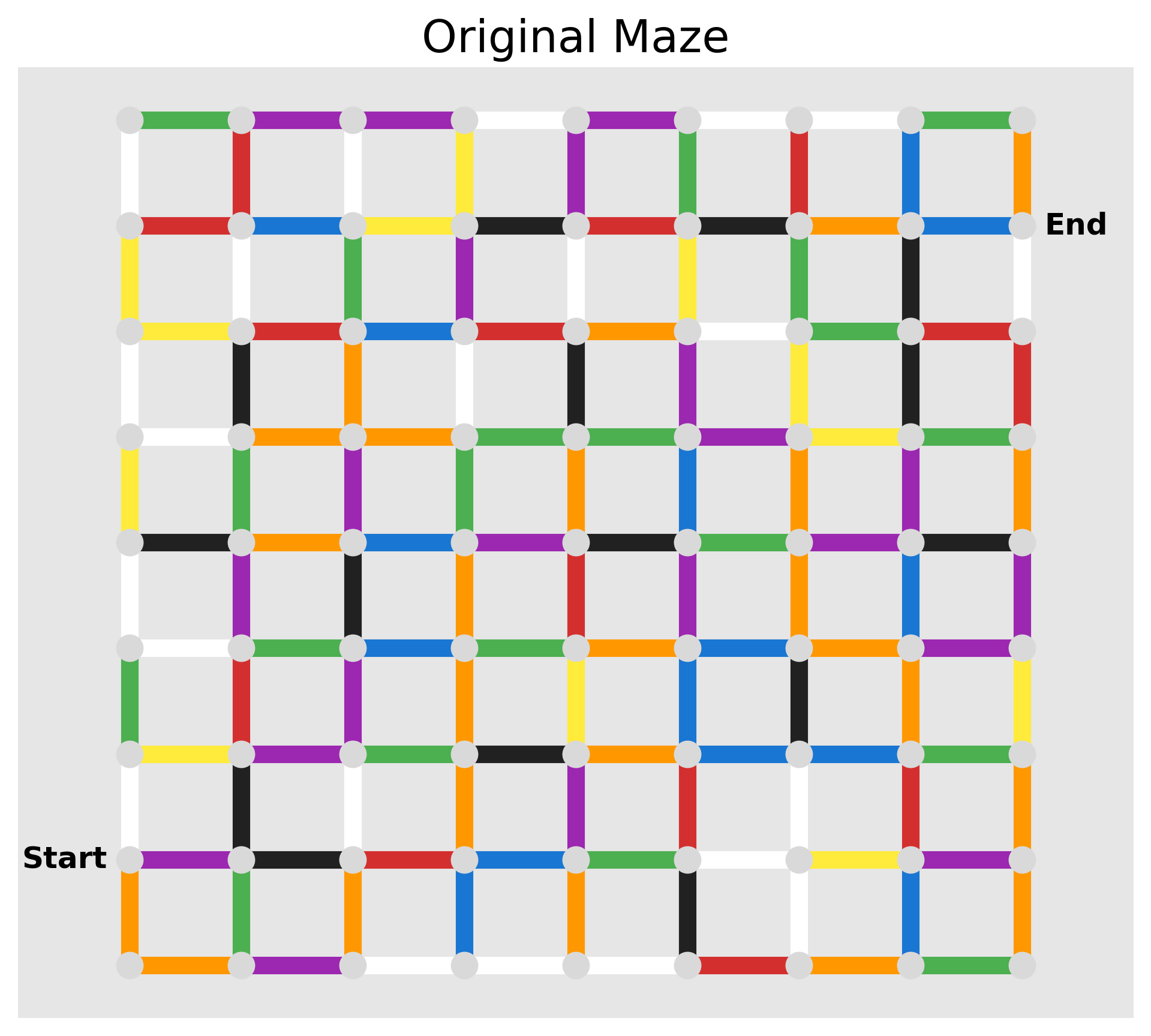
Solving the problem
Building the graph took time, but the initial work provides a significant advantage when it comes to solving the problem. In exchange for coding the network, we can use automated methods to solve for the shortest paths from start to finish.
Because we're only allowed to use certain colors to pass through the maze, we need a way to filter the valid and invalid paths. We will do this by creating subgraphs that contain only edges with the colors we want. Here's an example of filtering our graph for valid "blue" pathways, which can include edges that are blue, green, purple, or white.
G = create_graph()
subgraph = nx.Graph()
subgraph.add_edges_from([
(u, v) for u, v, d in G.edges(data=True) if d['color'] in COLORS['blue']
])
All we need to do now is call nx.shortest_path on our subgraph and we have our answer! Along with our plotting function from before, we can illustrate the paths to check our work. Here they are!
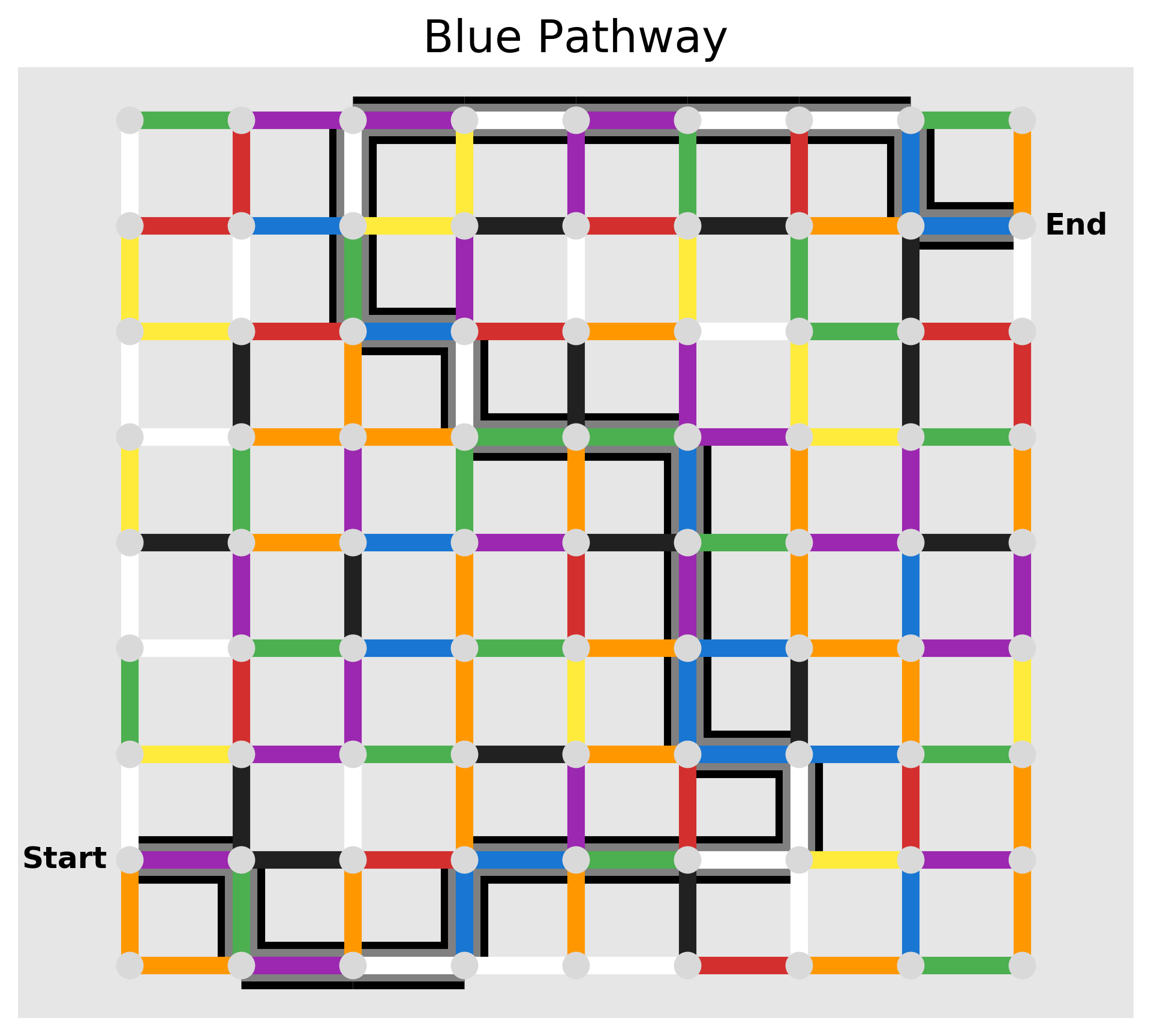
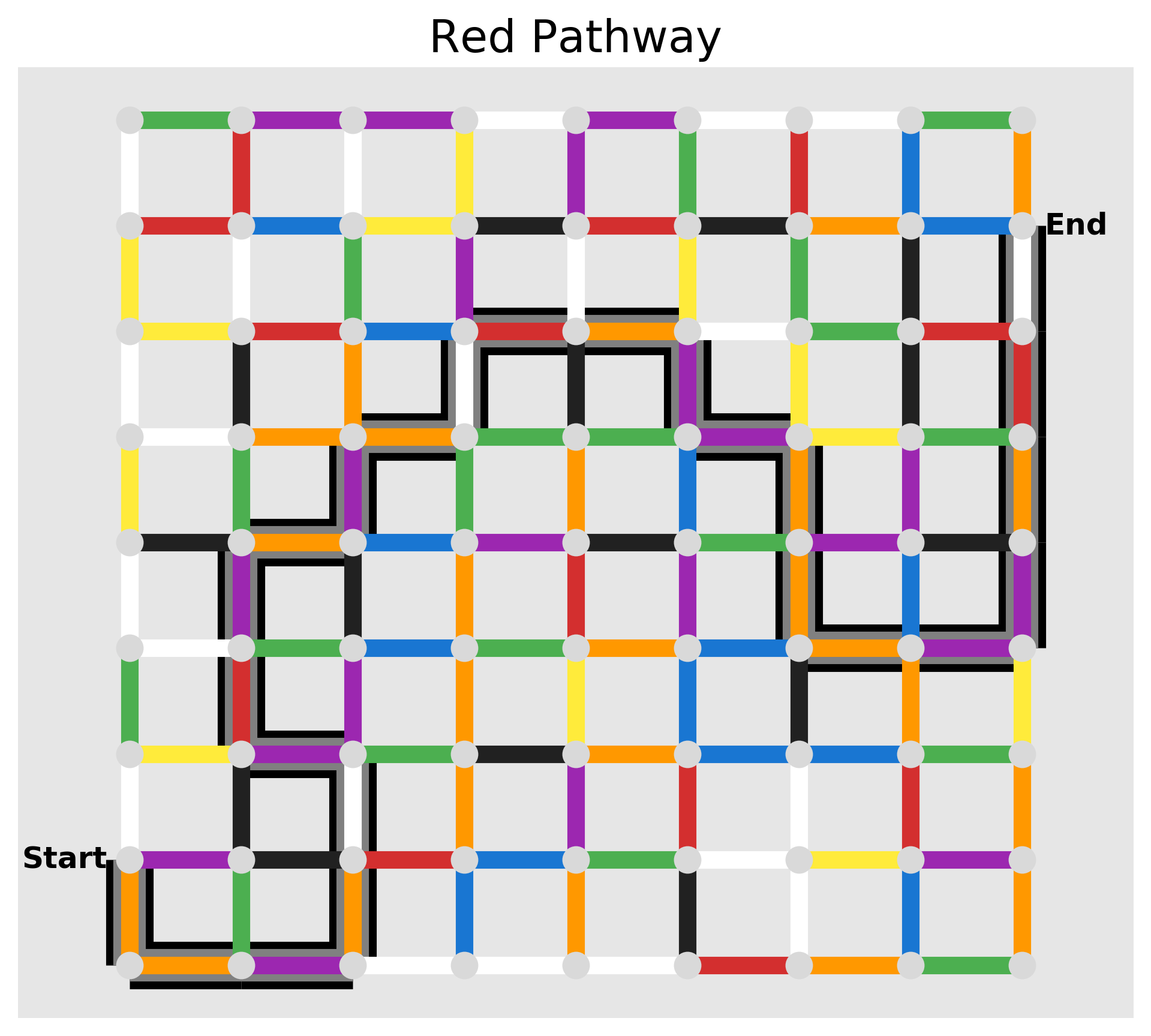
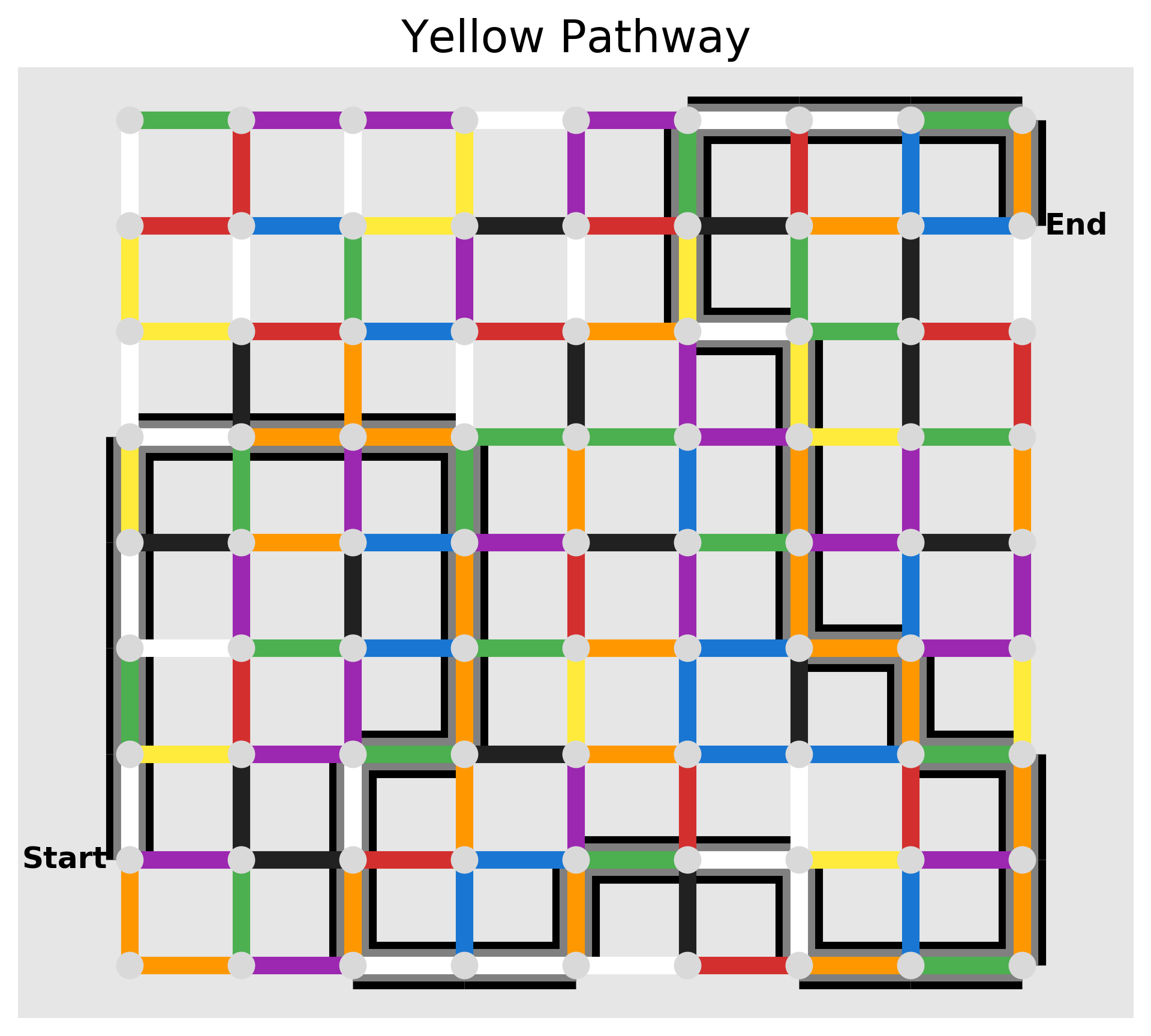
Full Code
The code below contains functions to build and visualize the maze, create subgraphs, and solve for the shortest path along a given color pathway.
# -*- coding: utf-8 -*-
"""
Solves the Riddler Express from 5-17-2019 using a networkx graph to specify
edge colors and solve for the shortest path along valid routes.
"""
import networkx as nx
import matplotlib.pyplot as plt
COLORS = {
'b': ['b', 'g', 'p', 'w'],
'y': ['y', 'g', 'o', 'w'],
'r': ['r', 'o', 'p', 'w'],
}
COLOR_MAP = {
'b': '#1976D2',
'o': '#FF9800',
'g': '#4CAF50',
'r': '#D32F2F',
'p': '#9C27B0',
'y': '#FFEB3B',
'w': '#FFFFFF',
'k': '#212121'
}
def color_pathway(graph, source=(0,1), target=(8,7), color='b'):
"""
Return the shortest path through a graph, given a "color pathway",
which can be "b" (blue), "y" (yellow), or "r" (red) from a source
node to a target node. The color pathway establishes a subgraph of
nodes and edges that contain related colors. The function returns
one pathway linking the source and target if it exists.
"""
subgraph = nx.Graph()
subgraph.add_edges_from([
(u, v) for u, v, d in graph.edges(data=True) if d['color'] in COLORS[color]
])
return nx.shortest_path(subgraph, source=source, target=target)
def plot_maze(graph, color=None):
"""
Plot the maze and optionally highlight the path along a specific color,
such as 'b', 'y', or 'r'. If color_pathway is None, no path will be
highlighted.
"""
fig, ax = plt.subplots(figsize=(8,7))
ax.set_facecolor('0.9')
ax.set_title('Riddler Maze')
# data for plotting
pos = {n: n for n in graph.nodes}
edge_color = [COLOR_MAP[d['color']] for u, v, d in graph.edges(data=True)]
# highlight the path for a given color if requested
if color is not None:
solution = color_pathway(graph, color=color)
nx.draw_networkx_edges(
graph, pos, edgelist=list(zip(solution, solution[1:])),
edge_color='k', width=19, ax=ax
)
nx.draw_networkx_edges(
graph, pos, edgelist=list(zip(solution, solution[1:])),
edge_color='0.5', width=13, ax=ax
)
# draw the original maze
nx.draw_networkx(
graph, pos, node_color='0.85', node_size=100, with_labels=False,
edge_color=edge_color, width=7, ax=ax
)
# annotation
ax.annotate('Start', (-0.2, 1), ha='right', va='center', fontsize=12, fontweight='bold')
ax.annotate('End', (8.2, 7), ha='left', va='center', fontsize=12, fontweight='bold')
# style
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
for s in ['top','right','left','bottom']:
ax.spines[s].set_visible(False)
ax.set_ylim(-0.5, 8.5)
ax.set_xlim(-1, 9)
return ax
def create_graph():
"""
Create the graph of the riddler express using coordinates as nodes
and identifying colors of edges using single letter codes. Lower
left corner is (0,0), and upper right corner is (8,8).
"""
G = nx.Graph()
# first column
G.add_edge((0,0), (0,1), color='o')
G.add_edge((0,1), (0,2), color='w')
G.add_edge((0,2), (0,3), color='g')
G.add_edge((0,3), (0,4), color='w')
G.add_edge((0,4), (0,5), color='y')
G.add_edge((0,5), (0,6), color='w')
G.add_edge((0,6), (0,7), color='y')
G.add_edge((0,7), (0,8), color='w')
# second column
G.add_edge((1,0), (1,1), color='g')
G.add_edge((1,1), (1,2), color='k')
G.add_edge((1,2), (1,3), color='r')
G.add_edge((1,3), (1,4), color='p')
G.add_edge((1,4), (1,5), color='g')
G.add_edge((1,5), (1,6), color='k')
G.add_edge((1,6), (1,7), color='w')
G.add_edge((1,7), (1,8), color='r')
# third column
G.add_edge((2,0), (2,1), color='o')
G.add_edge((2,1), (2,2), color='w')
G.add_edge((2,2), (2,3), color='p')
G.add_edge((2,3), (2,4), color='k')
G.add_edge((2,4), (2,5), color='p')
G.add_edge((2,5), (2,6), color='o')
G.add_edge((2,6), (2,7), color='g')
G.add_edge((2,7), (2,8), color='w')
# fourth column
G.add_edge((3,0), (3,1), color='b')
G.add_edge((3,1), (3,2), color='o')
G.add_edge((3,2), (3,3), color='o')
G.add_edge((3,3), (3,4), color='o')
G.add_edge((3,4), (3,5), color='g')
G.add_edge((3,5), (3,6), color='w')
G.add_edge((3,6), (3,7), color='p')
G.add_edge((3,7), (3,8), color='y')
# fifth column
G.add_edge((4,0), (4,1), color='o')
G.add_edge((4,1), (4,2), color='p')
G.add_edge((4,2), (4,3), color='y')
G.add_edge((4,3), (4,4), color='r')
G.add_edge((4,4), (4,5), color='o')
G.add_edge((4,5), (4,6), color='k')
G.add_edge((4,6), (4,7), color='w')
G.add_edge((4,7), (4,8), color='p')
# sixth column
G.add_edge((5,0), (5,1), color='k')
G.add_edge((5,1), (5,2), color='r')
G.add_edge((5,2), (5,3), color='b')
G.add_edge((5,3), (5,4), color='p')
G.add_edge((5,4), (5,5), color='b')
G.add_edge((5,5), (5,6), color='p')
G.add_edge((5,6), (5,7), color='y')
G.add_edge((5,7), (5,8), color='g')
# seventh column
G.add_edge((6,0), (6,1), color='w')
G.add_edge((6,1), (6,2), color='w')
G.add_edge((6,2), (6,3), color='k')
G.add_edge((6,3), (6,4), color='o')
G.add_edge((6,4), (6,5), color='o')
G.add_edge((6,5), (6,6), color='y')
G.add_edge((6,6), (6,7), color='g')
G.add_edge((6,7), (6,8), color='r')
# eighth column
G.add_edge((7,0), (7,1), color='b')
G.add_edge((7,1), (7,2), color='r')
G.add_edge((7,2), (7,3), color='o')
G.add_edge((7,3), (7,4), color='b')
G.add_edge((7,4), (7,5), color='p')
G.add_edge((7,5), (7,6), color='k')
G.add_edge((7,6), (7,7), color='k')
G.add_edge((7,7), (7,8), color='b')
# ninth column
G.add_edge((8,0), (8,1), color='o')
G.add_edge((8,1), (8,2), color='o')
G.add_edge((8,2), (8,3), color='y')
G.add_edge((8,3), (8,4), color='p')
G.add_edge((8,4), (8,5), color='o')
G.add_edge((8,5), (8,6), color='r')
G.add_edge((8,6), (8,7), color='w')
G.add_edge((8,7), (8,8), color='o')
# first row
G.add_edge((0,0), (1,0), color='o')
G.add_edge((1,0), (2,0), color='p')
G.add_edge((2,0), (3,0), color='w')
G.add_edge((3,0), (4,0), color='w')
G.add_edge((4,0), (5,0), color='w')
G.add_edge((5,0), (6,0), color='r')
G.add_edge((6,0), (7,0), color='o')
G.add_edge((7,0), (8,0), color='g')
# second row
G.add_edge((0,1), (1,1), color='p')
G.add_edge((1,1), (2,1), color='k')
G.add_edge((2,1), (3,1), color='r')
G.add_edge((3,1), (4,1), color='b')
G.add_edge((4,1), (5,1), color='g')
G.add_edge((5,1), (6,1), color='w')
G.add_edge((6,1), (7,1), color='y')
G.add_edge((7,1), (8,1), color='p')
# third row
G.add_edge((0,2), (1,2), color='y')
G.add_edge((1,2), (2,2), color='p')
G.add_edge((2,2), (3,2), color='g')
G.add_edge((3,2), (4,2), color='k')
G.add_edge((4,2), (5,2), color='o')
G.add_edge((5,2), (6,2), color='b')
G.add_edge((6,2), (7,2), color='b')
G.add_edge((7,2), (8,2), color='g')
# fourth row
G.add_edge((0,3), (1,3), color='w')
G.add_edge((1,3), (2,3), color='g')
G.add_edge((2,3), (3,3), color='b')
G.add_edge((3,3), (4,3), color='g')
G.add_edge((4,3), (5,3), color='o')
G.add_edge((5,3), (6,3), color='b')
G.add_edge((6,3), (7,3), color='o')
G.add_edge((7,3), (8,3), color='p')
# fifth row
G.add_edge((0,4), (1,4), color='k')
G.add_edge((1,4), (2,4), color='o')
G.add_edge((2,4), (3,4), color='b')
G.add_edge((3,4), (4,4), color='p')
G.add_edge((4,4), (5,4), color='k')
G.add_edge((5,4), (6,4), color='g')
G.add_edge((6,4), (7,4), color='p')
G.add_edge((7,4), (8,4), color='k')
# sixth row
G.add_edge((0,5), (1,5), color='w')
G.add_edge((1,5), (2,5), color='o')
G.add_edge((2,5), (3,5), color='o')
G.add_edge((3,5), (4,5), color='g')
G.add_edge((4,5), (5,5), color='g')
G.add_edge((5,5), (6,5), color='p')
G.add_edge((6,5), (7,5), color='y')
G.add_edge((7,5), (8,5), color='g')
# seventh row
G.add_edge((0,6), (1,6), color='y')
G.add_edge((1,6), (2,6), color='r')
G.add_edge((2,6), (3,6), color='b')
G.add_edge((3,6), (4,6), color='r')
G.add_edge((4,6), (5,6), color='o')
G.add_edge((5,6), (6,6), color='w')
G.add_edge((6,6), (7,6), color='g')
G.add_edge((7,6), (8,6), color='r')
# eighth row
G.add_edge((0,7), (1,7), color='r')
G.add_edge((1,7), (2,7), color='b')
G.add_edge((2,7), (3,7), color='y')
G.add_edge((3,7), (4,7), color='k')
G.add_edge((4,7), (5,7), color='r')
G.add_edge((5,7), (6,7), color='k')
G.add_edge((6,7), (7,7), color='o')
G.add_edge((7,7), (8,7), color='b')
# ninth row
G.add_edge((0,8), (1,8), color='g')
G.add_edge((1,8), (2,8), color='p')
G.add_edge((2,8), (3,8), color='p')
G.add_edge((3,8), (4,8), color='w')
G.add_edge((4,8), (5,8), color='p')
G.add_edge((5,8), (6,8), color='w')
G.add_edge((6,8), (7,8), color='w')
G.add_edge((7,8), (8,8), color='g')
return G
if __name__ == '__main__':
G = create_graph()
blue = color_pathway(G, color='b')
yellow = color_pathway(G, color='y')
red = color_pathway(G, color='r')
plot_maze(G)
plot_maze(G, color='b')
plot_maze(G, color='r')
plot_maze(G, color='y')