Riddler Counterfeits
Aug 23, 2019
Introduction
This week's fivethirtyeight riddler was created by yours truly! It was the first puzzle I've submitted to the riddler, and I hope you enjoyed it. This week we attempt to fool a bank with counterfeit hundred dollar bills. Here is the full text.
You are an expert counterfeiter, and you specialize in forging one of the most ubiquitous notes in global circulation, the U.S. $100 bill. You’ve been able to fool the authorities with your carefully crafted C-notes for some time, but you’ve learned that new security features will make it impossible for you to continue to avoid detection. As a result, you decide to deposit as many fake notes as you dare before the security features are implemented and then retire from your life of crime.You know from experience that the bank can only spot your fakes 25 percent of the time, and trying to deposit only counterfeit bills would be a ticket to jail. However, if you combine fake and real notes, there’s a chance the bank will accept your money. You have $2,500 in bona fide hundreds, plus a virtually unlimited supply of counterfeits. The bank scrutinizes cash deposits carefully: They randomly select 5 percent of the notes they receive, rounded up to the nearest whole number, for close examination. If they identify any note in a deposit as fake, they will confiscate the entire sum, leaving you only enough time to flee.
How many fake notes should you add to the $2,500 in order to maximize the expected value of your bank account? How much free money are you likely to make from your strategy?
Solution
The counterfeiter wants to strike the optimum balance between profitability and risk. The ideal strategy will include as many fake notes as possible to maximize the size of the deposit, but not so many that the bank becomes aware of the fraud and seizes everything.
The ideal strategy is to add 55 fake notes to the 25 real notes for a total deposit of $8000. The expected gain from this strategy is $1256†, which is the weighted average of expected profit from successful deposits and expected losses from bank seizures. With 55 fake notes, there is a 47% chance we avoid detection and collect a profit of $5500 - the value of the fake notes we were able to sneak into circulation. (Remember we started with $2500, so only the fake notes count as profit.) There is a 53% chance we are caught by the bank and lose the $2500 in real dollars we used as decoys.
† A note on interpreting the results: I intended the problem to include the risk of losing $2500 if we are caught, and gaining the value of the fake notes if we are not. Therefore, the expected value would be . However, potentially to avoid some ambiguity, the problem was rewritten to ask "how much free money are you likely to make from your strategy?" I believe with that criteria, the answer should be , which includes only the value of the fake notes, and doesn't penalize losing the real ones. Another interpretation could count the original $2500 as free money as well (perhaps because it may have been the product of fraud at one point or another too!), for an answer of . I think all three are reasonable interpretations of the problem, but the first method is my favorite, so I'll continue that way.
How can we be sure no other strategy produces a higher profit? For example, suppose we combine 30 fake notes with 25 real notes instead. The bank will select three notes for its audit, which is 5% of 55, rounded up to the nearest whole number. Depending on our luck, the bank could choose all three fake notes, all three real notes, or some combination in between.
Let’s assume the bank randomly chooses two fake notes and one real note for its audit. This occurs with roughly 41.5% probability, given by the formula . Each fake note is detected 25% of the time, which means at least one fake note from the pool of two is detected of the time. We use similar logic to solve for the likelihood and detection rate of the audits with three fakes, one fake, and zero fake notes. The overall detection rate is equal to the weighted average across each potential audit.
For the 30 fake, 25 real strategy, the probability of success is 64.3%, and the probability of detection is 35.7%. Therefore, the expected profit is . That’s a decent payday, but we can do better. The chart below shows the profit for strategies with up to 200 fake notes, and it confirms the maximum is achieved when we use 55.
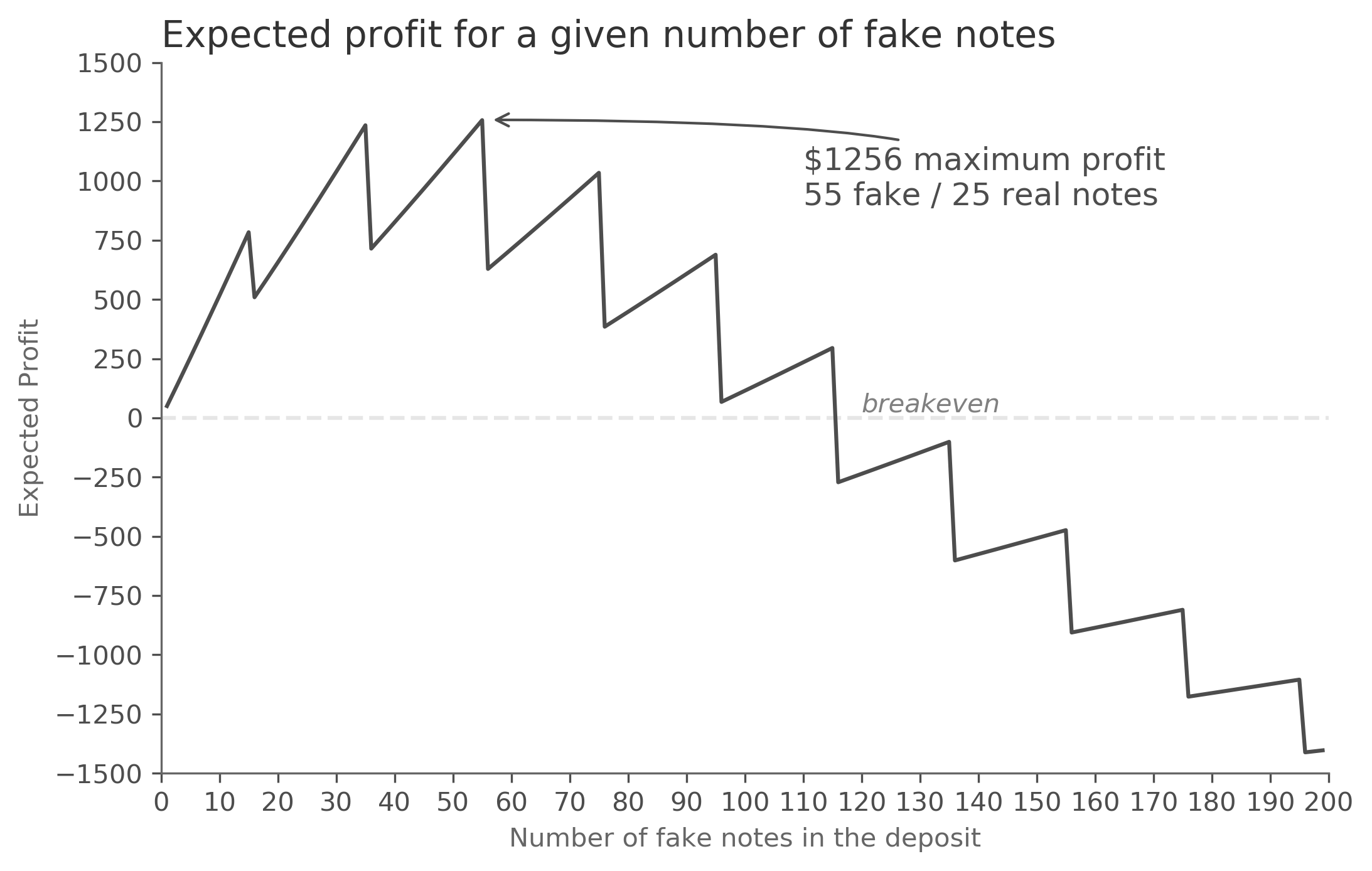
We can see two patterns above. First, as we move to the right, we enter the “greedy danger zone,” where the bank becomes more likely to discover our fraud and seize the starting capital, resulting in larger and larger expected losses. Second, we see a sawtooth behavior caused by the bank’s practice of auditing 5% of deposited notes. The effect is significant: 55 is the ideal answer because we deposit 80 total notes, resulting in the bank auditing four. If we use 56 fake notes for a total of 81, then the bank audits five instead, which cuts the expected gain in half! A life of crime only pays if you’re good with numbers.
Full Code
The code this week is comprised of a single function that returns the expected value of a strategy with fake notes and real notes. There are optional parameters for the number of notes selected in an examination, the accuracy of the bank in detecting fake notes, and the denomination of bill used, with defaults set per the question. To generate a chart, run this model for the desired range of fake notes, e.g. 1 through 200, and plot the results.
import numpy as np
from math import ceil
from scipy.special import comb
def model(n_fake, n_real, selected=0.05, accuracy=0.25, denomination=100):
"""
Calculate the expected value of a strategy with n fake bills and m real bills.
Final expected value is defined as
* the value of the fake notes times the probability of not being caught
* minus the value of the real notes times the probability of being caught.
Parameters
----------
n_fake : int > 0, the number of fake bills used
n_real : int > 0, the number of real bills used
selected : float, between 0 and 1, the percent of bills examined by the bank,
which will be applied to (n_fake + n_real), then rounded up to the nearest
whole number
accuracy : float, between 0 and 1, the likelihood of a bank detecting a fake
note, given that it is examining that note
denomination : int, the bill in question, e.g. $100, to multiply the result
Returns
-------
expected_value : float, the expected value of the given strategy
Examples
--------
>>> model(n_fake=55, n_real=25, selected=0.05, accuracy=0.25, denomination=100)
1256.8909531923773
"""
# number of notes randomly selected for inspection (rounded up to nearest whole)
k = ceil((n_fake+n_real)*selected)
# probabilities of choosing 0 through x fake notes in an examination
# calculated by solving for the denominator and numerator separately,
# then the (n choose k) component of each examination, and finally by
# multiplying all three together for an overall likelihood factor.
denominator = np.array([n_real+n_fake-x for x in range(k)])
numerator = np.array([
[n_fake - a for a in range(k-x)] + [n_real - b for b in range(x)]
for x in range(k+1)
])
combinations = np.array([comb(k, x) for x in range(k+1)])
factor = combinations * (numerator / denominator).prod(1)
# final likelihood of detection and corresponding expected value of payoffs
likelihood = np.array([(1-accuracy)**(k-x) for x in range(k+1)])
payoff = n_fake*likelihood - n_real*(1-likelihood)
return (factor * payoff * denomination).sum()