Riddler Delirious Ducks
Jan 17, 2020
Introduction
This week's Riddler Classic is a delightful diversion - tracking delirious ducks as they randomly swim from rock to rock in a pond. How long will it take them to end up on the same rock? We'll use markov chains in Python to solve it.
After a long night of frivolous quackery, two delirious ducks are having a difficult time finding each other in their pond. The pond happens to contain a 3×3 grid of rocks.Every minute, each duck randomly swims, independently of the other duck, from one rock to a neighboring rock in the 3×3 grid — up, down, left or right, but not diagonally. So if a duck is at the middle rock, it will next swim to one of the four side rocks with probability 1/4. From a side rock, it will swim to one of the two adjacent corner rocks or back to the middle rock, each with probability 1/3. And from a corner rock, it will swim to one of the two adjacent side rocks with probability 1/2.
If the ducks both start at the middle rock, then on average, how long will it take until they’re at the same rock again? (Of course, there’s a 1/4 chance that they’ll swim in the same direction after the first minute, in which case it would only take one minute for them to be at the same rock again. But it could take much longer, if they happen to keep missing each other.)
Extra credit: What if there are three or more ducks? If they all start in the middle rock, on average, how long will it take until they are all at the same rock again?
Solution
Fortunately, the pond is small enough that our delirious ducks are expected to meet each other less than five minutes after they start swimming: 4.905 minutes, to be exact. Of course, because the process is random, they could end up swimming for quite some time, but this answer reflects the average of all potential random outcomes.
Methodology
We can use Markov Chains to solve this problem - a highly effective tool in our probabilistic arsenal that I've used several times before. In a markov chain, we specify the probability of moving from one state to the next - in this case, from one rock in the pond to the next.
Because there are two ducks, each state will need to encode both ducks' positions. We can exploit the rotational symmetry of the problem and cover all possible positions with just five states, shown below. Each blue box represents the position of one duck (it doesn't matter which duck.)
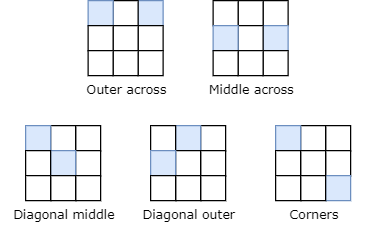
Note that the ducks will never be in adjacent squares (for example, the top left square and the top middle square) because of the parity of this problem. The ducks can't move diagonally, so they shift between the diamond squares (middle of each edge) and the other squares each time they swim. This vastly simplifies the number of states we need to model. (If the ducks could randomly decide not to swim and to stay on their current rock, then the problem loses this parity and becomes more complex.)
Once we specify the states, we need to calculate the probability of moving from one state to the next, including the probability of arriving at the same rock. When they arrive at the same rock, we call this the absorbing state, and the markov chain stays there forever. Fortunately, we can use some clever math to solve for the expected amount of time it takes to arrive in the absorbing state, and that gives us our answer.
The probabilities of moving from state to state are encoded in a transition matrix, which allows us to calculate the time it takes for our ducks to meet again after starting. We use numpy to create this matrix, where each row is the starting state, and each column is a potential ending state.
import numpy as np
M = np.array([
[0.0, 1/4, 0.0, 0.0, 1/2, 0.0, 1/4], # start
[0.0, 0.0, 2/9, 4/9, 0.0, 2/9, 1/9], # middle across
[0.0, 1/4, 0.0, 0.0, 1/2, 0.0, 1/4], # outer edge across
[0.0, 1/4, 0.0, 0.0, 1/2, 0.0, 1/4], # diagonal including middle
[0.0, 0.0, 2/9, 4/9, 0.0, 1/9, 2/9], # diagonal excluding middle
[0.0, 1/2, 0.0, 0.0, 1/2, 0.0, 0.0], # opposite corners
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 1.0], # absorbing state
])
Each row of the matrix sums to 1, because it specifies the probabilities of moving from a given state to all other states. Once we arrive in the absorbing state, the probability of staying there is 100%. With some linear algebra we can solve for the number of steps it takes to move from the starting position to the absorbing state.
>>> np.linalg.inv(np.eye(6) - M[:-1, :-1]).sum(1)
array([4.90540541, 5.67567568, 4.90540541, 4.90540541, 4.97297297,
6.32432432])
The output array tells us how many steps it takes to get from each state to the absorbing state. We see it takes 4.905 steps from the start position, 5.676 steps from the "middle across" position, and so on. Interestingly, the "outer across" and "diagonal middle" states have the exact same answer as the starting position, meaning that if the ducks started in those configurations the answer would be unchanged.
In the future I hope to tackle the extra credit portion of this problem, but I'm running short of time this weekend. I think exploiting the parity of the problem will be a key element of solving this without explicitly listing all possible arrangements of ducks. Stay tuned!